
-내 생각
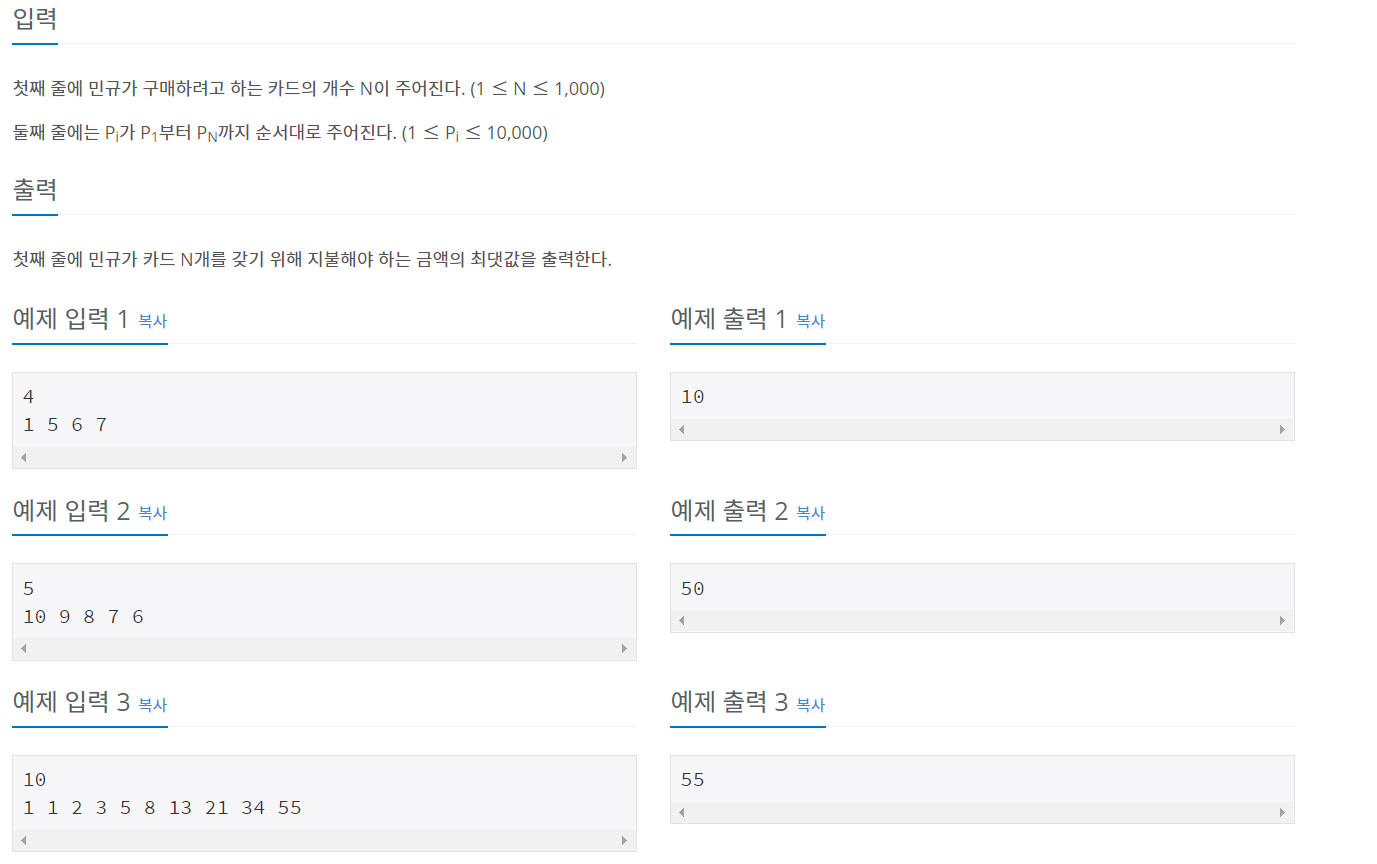
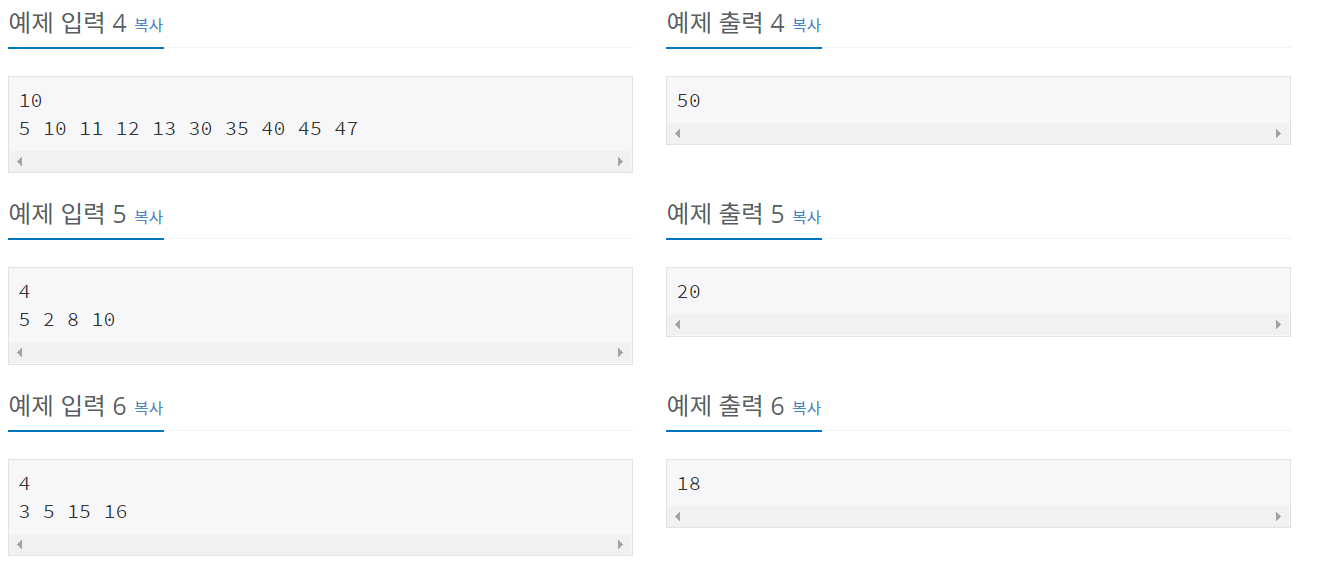
이 문제의 경우 문제 지문이 상당히 길기 때문에 자칫 어렵게 보일 수 있는데, 그렇게 어려운 문제는 아니라고 생각한다. 문제의 요점을 잘 읽어보면 카드의 개수와 1 ~ n개의 카드팩으로 이루어진 가격 p1 ~ pn이 주어질 때 카드 개수를 살 수 있는 최댓값을 구하는 것이 문제의 요지이다. 즉, 예제 입력 1의 경우 4개의 카드를 사고자 할 때, 카드 1개로 이루어진 p1의 가격, 카드 2개로 이루어진 p2의 가격, 3개로 이루어진 p3의 가격 4개로 이루어진 p4의 가격이 주어지고, 어떤 카드팩을 골라야 최대 비용으로 구매할 수 있는지 묻는 것이다.
처음 접근은 역시 dp테이블을 만든 후 각 경우의 수를 따져보는 것이었다. 즉 카드를 4장 구매하고 싶다고 할 때, 각 가격별로 카드를 1장 살 때, 2장 살 때... 4장 살 때의 가격으로 테이블을 채워보니 규칙성이 눈에 보였다. 첫 접근만에 맞출 수 있었다.
-해법
위에도 언급했듯이 카드별로 구매할 수 있는 최댓값을 알기위해 테이블을 그린다. 아래가 그 테이블이다. (예제 입력 1 기준 테이블)
우선 n만큼 카드의 가격이 주어지므로 테이블은 정사각형 모양이다. p1을 이용해서 각 카드 수를 구매하는 값을 구해보면 p1 * 카드의 수가 된다는 것은 알 수 있다. (단위는 임의로 원을 사용하겠다.) 이런식으로 단순한 공식을 통해 모든 칸을 채울 수 있는 경우가 보통의 dp테이블에서 초기화 값이 된다.
| 카드 1장 | 카드 2장 | 카드 3장 | 카드 4장 | |
| 1 (=p1) | 1원 | 2원 | 3원 | 4원 |
| 5 (=p2) | ||||
| 6 (=p3) | ||||
| 7 (=p4) |
다음으로 p2를 이용해서 카드를 구매할 때이다. 카드가 1장일 경우는 살 수없다. p2에는 카드가 2장 들어있으므로, 카드가 2장일 경우는 p2와 동일한 개수이므로 p2만 사면 모두 살 수 있다.
문제는 카드가 3장일 때이다. 3장인 경우는 p2의 수를 초과하므로 남는만큼 다른 카드팩을 골라야 한다. 현시점에서 존재하는 카드팩은 p1과 p2밖에 없으므로 우선 p2로 한 팩을 사면 남는 카드는 1장이다. 그렇다면 카드 1장으로 살 수 있는 경우는 카드 1장 열을 확인하면 된다. 이 중 최댓값은 1원이므로 p1을 한 팩 사서 p2 + p1팩으로 3장을 만들 수 있다.
마지막으로 카드가 4장일 경우, p2팩으로 우선 한 번 사면, 2장의 카드를 더 살 수 있다. 그렇다면 카드 2장열을 탐색해 최댓값을 가지고 있는 경우를 찾는다. 물론 자기 자신도 포함해야 한다. 남은 2장을 p1으로 살 경우 2원이 되고, p2로 살 경우 5원이므로 2원 <5원이 된다. 그러므로 p2 + p2를 통해서 10원을 도출할 수 있다.
| 카드 1장 | 카드 2장 | 카드 3장 | 카드 4장 | |
| 1 (=p1) | 1원 | 2원 | 3원 | 4원 |
| 5 (=p2) | 0원 | 5원 | 6원 | 10원 |
| 6 (=p3) | ||||
| 7 (=p4) |
다음으로 p3의 경우를 보자. 마찬가지로 3장까지는 0원이 채워질 것이다. 3장이 들어있기 때문에, 3장의 경우는 p3한 팩이면 남는 카드가 없으므로 6원으로 구매가 가능하다. 마지막으로 4장의 경우는 p3를 한 팩 산 이후, 1장이 남게 되는데 1장으로 살 수 있는 최댓값의 경우는 p1을 구매하는 것이다. 그러므로 자기 자신인 6원 +1원 = 7원이 된다.
| 카드 1장 | 카드 2장 | 카드 3장 | 카드 4장 | |
| 1 (=p1) | 1원 | 2원 | 3원 | 4원 |
| 5 (=p2) | 0원 | 5원 | 6원 | 10원 |
| 6 (=p3) | 0원 | 0원 | 6원 | 7원 |
| 7 (=p4) |
마지막으로 p4의 경우는 4장을 사면 남는 카드가 없기 때문에 자기 자신의 값만 존재하게 된다.
| 카드 1장 | 카드 2장 | 카드 3장 | 카드 4장 | |
| 1 (=p1) | 1원 | 2원 | 3원 | 4원 |
| 5 (=p2) | 0원 | 5원 | 6원 | 10원 |
| 6 (=p3) | 0원 | 0원 | 6원 | 7원 |
| 7 (=p4) | 0원 | 0원 | 0원 | 7원 |
이렇게 완성된 표를 확인해보면 각 카드 장 수에서 구매할 수 있는 최댓값이 나와있다. 우리가 원하는 것은 4장일 경우의 최댓값이므로 카드가 4장일 때, 모든 행을 탐색해보면 p2 + p2가 10원으로 최댓값이라는 것을 알 수 있다.
이를 통해 유추할 수 있는 점화식을 세워보면,
// N은 N번 째 카드팩의 카드 장 수(카드팩의 순서), K는 카드의 장 수라 할 때,
DP[N][K] = Math.max( DP [1][K-N], DP [2][K-N],...., DP [N][K-N]) + COST [N]이라 할 수 있다.
import java.util.*;
import java.math.*;
public class Main {
static int dp[][],cost[];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
// DP[카드팩 순서][카드 장 수]
dp = new int[n+1][n+1];
// COST[카드팩 순서]
cost = new int[n+1];
for(int i=1;i<=n;i++) { // 카드팩 순서에 맞게 가격을 입력
cost[i] = sc.nextInt();
}
for(int i=1;i<=n;i++) { // DP의 1번행은 1장이 들어있는 카드 팩 가격 * 카드 장 수로 초기화
dp[1][i] = cost[1]*i;
}
for(int i=2;i<=n;i++) {
for(int j=i;j<=n;j++) { // 행과 열을 고정, 값의 입력을 위해
int max =Integer.MIN_VALUE; // 최댓값을 찾는 과정
if(j-i !=0) { // 카드 장 수 - 팩의 순서 >0 인 경우 고려해주어야 한다.
// 즉, 4장일 때, 2번 째 팩을 샀을 때 남는 카드 장 수를 의미
for(int k=1;k<=j-i;k++) { // 1번 팩 부터 자기 자신의 팩까지만 반복하면 된다.
// 표를 통해 확인 가능
if(dp[k][j-i]>max) { // 최댓값 찾기
max = dp[k][j-i];
}
}
}else if(j-i ==0) max = 0; // 카드 장 수 - 팩의 순서인 경우, 즉 카드가 2장일 때,
// 2번 팩을 고르면 2-2으로 0이 된다. 즉 더해줄 값이 없다.
dp[i][j] = cost[i] + max; // 위에서 구한 MAX과 자기 자신의 가격을 더한다.
}
}
int max =Integer.MIN_VALUE;
for(int i=1;i<=n;i++) { // N번 째 열의 모든 값을 탐색
if(dp[i][n]>max) // 최댓값을 찾는다.
max = dp[i][n];
}
System.out.println(max);
}
}