![[백준,BOJ 2011] 암호코드( JAVA 구현)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FC23TP%2FbtqAdb7hqDj%2FvlvVLq7AOKh2MFHFjBPwl0%2Fimg.png)
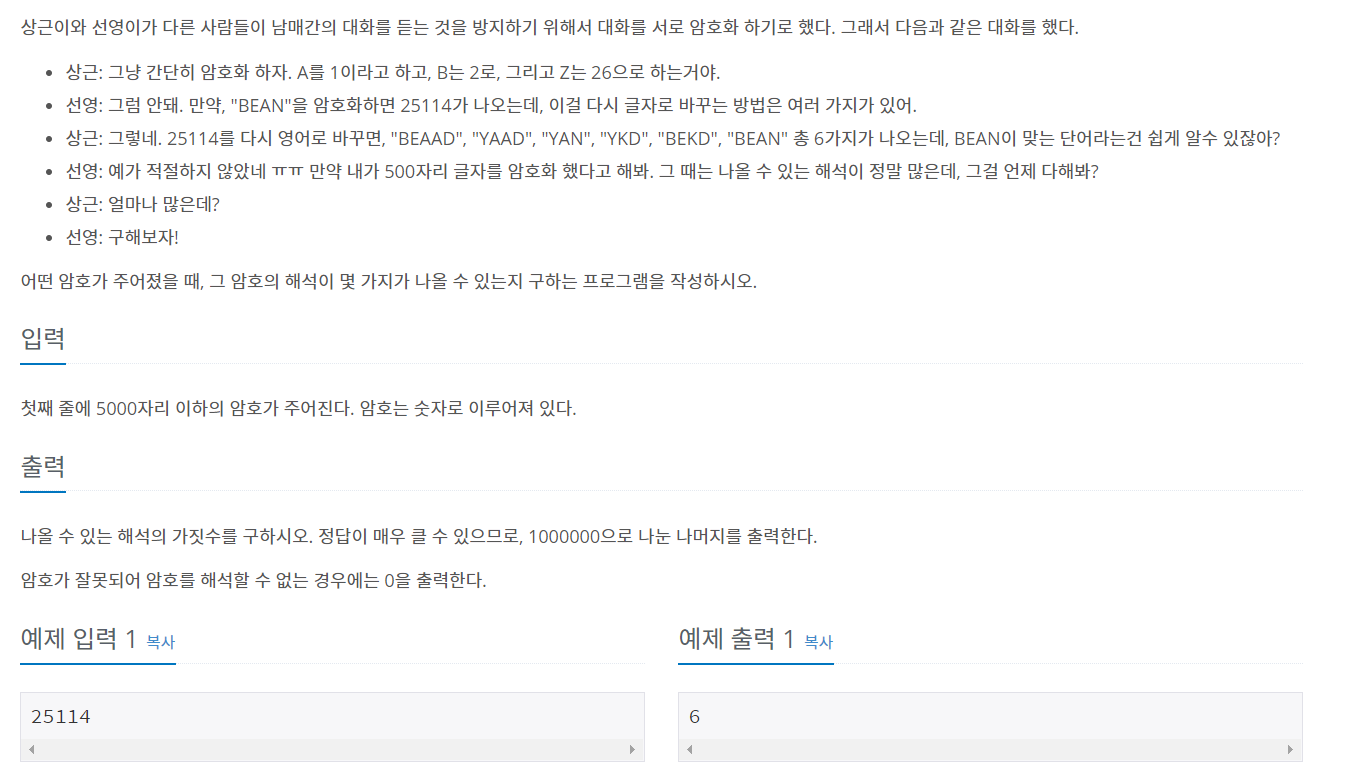
-내 생각
처음 문제를 풀 때, dp테이블을 그려보려 했는데 감이 잡히질 않았고, 어떻게 풀어야 할지 감이 잡히지 않아 여러 방법으로 시도해보았는데 풀리지 않았다. 특정 예시를 들어서 테이블을 그려야 했었는데, 처음에 그릴 때, 입력값인 암호가 1일 경우 A, 2일 경우 B,... 11일 경우 AA, K.. 같은 방식으로 생각해서 접근이 불가능했었다.
-해법
이 문제의 경우 푸는 방식이 다른 DP들과 별로 다르지 않았다. 우선 입력 예제 25114로 예시를 들면, DP에서 많이 썼던, 각 글자를 마지막 숫자로 보는 방식이다. 즉 2부터 2가 마지막으로 오는 경우의 수를 구하고, 다음 5가 마지막으로 오는 경우의 수를 구하고 와 같은 방식이다. 그러나 이 문제에서는 주의해야 할 점이, 1부터 26까지의 숫자에 알파벳을 부여해 사용하므로 각 숫자들이 가능한 범이가 정해져 있다. 이 말은 자리 수가 1개인 경우와 2개인 경우를 모두 고려해 주어야 한다는 점이다. 그중에서도 두 자릿수는 26까지의 범위가 존재한다.
위와 같은 조건으로 다시 마지막 수라고 생각해본다면, 우선 2가 마지막 수이면서 한 자리로 사용된 경우 + 2가 마지막 수이면서 두 자리로 사용 된 경우를 따져야 한다. 지금은 2밖에 없기 때문에 앞자리에 숫자가 존재하지 않는다. 그러므로 두 자릿수로 사용하는 것은 불가능하고 한 자리로 사용하면 B 한 가지가 존재하게 되므로 1+0 = 1이 된다. 이 문제도 표를 그려보면서 나가보자 아래가 그 표이다.
| 암호 | 한 자리수인 경우 | 두 자리수인 경우 |
| 2 | 1 | 0 |
| 5 | ||
| 1 | ||
| 1 | ||
| 4 |
이 경우는 2뿐만 아니라 모든 숫자가 처음에 오는 경우는 모두 동일하다. 숫자 한 개가 무엇이 오든 한 자리 수의 경우는 1이 될 것이고, 두 자릿수는 앞자리에 숫자가 없으므로 0이 고정이다. ( 그러나 문제에서 0은 사용하지 않는다 했으므로 0은 제외이다.) 이렇게 고정된 값이 DP 배열의 초기값이 되는 것이다.
다음으로 5가 마지막으로 오는 경우 중 한 자리인 경우와 두 자리인 경우를 보자.
5가 마지막으로 오는 경우 중 한 자리 수로 사용되는 경우 5가 한 자리로 사용되었으므로, 5 앞으로는 2가 한 자리 수의 경우 + 두 자리 수의 경우가 될 것이다. 그러나 2가 두 자릿수로 사용될 수는 없으므로 0이 되고 한 자리 수로 사용되는 경우는 1이므로 1+0 = 1이 된다.
5가 마지막으로 오는 경우 중 두 자리수로 사용되는 경우는 5 이전의 숫자 2가 존재하므로 25를 하나로 보게 되면, 5 전의 전을 고려해주어야 하는데, 이 경우는 DP [0][0] 과 DP[1][0]인 경우다. 이러한 경우를 채워주기 위해 DP[0][0]은 1로 채워준다. (암호화 할 수 없는 경우를 한 가지로 보는 것) 그렇다면 DP[0][0] + DP [0][1] = 1이므로 표로 나타내면,
| 암호 | 한 자리수인 경우 | 두 자리수인 경우 |
| 2 | 1 | 0 |
| 5 | 1 | 1 |
| 1 | ||
| 1 | ||
| 4 |
다음으로 1이 마지막으로 오는 경우 중 한 자릿수로 사용한 경우, 1의 앞으로 25를 이용한 경우의 수가 올 것이다. 이것은 위에 언급했듯이 한 자리 수의 경우 + 두 자리 수의 경우이므로 1+1 =2가 된다.
두 자리수로 사용되는 경우는 1의 앞의 숫자가 5이므로 26의 범위를 벗어나게 되므로 0이 된다.
| 암호 | 한 자리수인 경우 | 두 자리수인 경우 |
| 2 | 1 | 0 |
| 5 | 1 | 1 |
| 1 | 2 | 0 |
| 1 | ||
| 4 |
마지막 예로 두 번째 1이 마지막에 올 경우, 한 자리로 사용하면 앞자리는 251의 경우의 수인 2+0=2가 올 것이고, 두 자리 수로 사용되는 경우는 앞자리가 1이므로 11이 되어 조건에 부합되므로 자신의 이전 이전을 고려해주어야 한다. 이전 이전의 숫자는 2와 5를 이용한 경우의 수이므로 1+1 =2가 된다.
| 암호 | 한 자리수인 경우 | 두 자리수인 경우 |
| 2 | 1 | 0 |
| 5 | 1 | 1 |
| 1 | 2 | 0 |
| 1 | 2 | 2 |
| 4 |
그냥 하는 김에 4까지 해보면, 4가 마지막으로 오는 경우의 수 중 한 자리로 사용할 경우, 4 앞으로 2511을 이용해 채울 수 있는 경우의 수는 이전에 구해놓은 2+2=4가 된다. 두 자리 수로 사용 할 경우 앞자리가 1이므로 14로 조건에 만족하므로 이전 이전인 251을 이용해 채울 수 있는 경우의 수를 따지면, 2+0으로 2가 된다.
| 암호 | 한 자리수인 경우 | 두 자리수인 경우 |
| 2 | 1 | 0 |
| 5 | 1 | 1 |
| 1 | 2 | 0 |
| 1 | 2 | 2 |
| 4 | 4 | 2 |
이렇게 완성된 표의 마지막 행에 최종 경우의 수가 쌓인다. 두 경우의 수를 더해주어야 답이 되므로 4+2 =6이 되는 것이다.
위의 과정을 통해 점화식을 도출해보면, 조건을 만족할 때!!!! (이 문제에서는 조건이 중요하다 예외가 많기 때문에)
DP [n][0] = dp [n-1][0] + dp [n-1][1] // 한 자리 수로 사용하는 경우
DP [n][1] = dp [n-2][0] + dp [n-2][1] // 두 자리 수로 사용하는 경우
최종 경우의 수는 두 경우의 수를 합친, ans = dp [n][0] + dp [n][1]이 된다.
마지막으로 고려해주어야 할 예외처리의 경우,
1. 0만 입력된 경우 = 바로 0 출력 후 프로그램 종료 (위의 과정 불필요)
2. 두 자리 수인 경우를 고려할 때, 현재 자리가 0~9인 경우는 => 앞자리가 1이 가능
현재 자리가 0~6인 경우는 => 앞 자리가 2가 가능
3. 00인 경우는 불가능하므로 0 출력 후 프로그램 종료
import java.util.*;
import java.math.*;
public class Main {
static int dp[][];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String code = sc.next();
dp = new int [code.length()+1][2]; // 0: 끝자리가 한 자리, 1: 끝자리가 두 자리
//dp배열 초기화
dp[1][0] = 1; dp[1][1] =0;
dp[0][0] = 1; dp[0][1] =0;
//0입력 시 종료
if(code.charAt(0)-'0' == 0) {
System.out.println("0");
return;
}
for(int i=2;i<=code.length();i++) {
if(code.charAt(i-1)-'0'==0) { // 자기 자신이 0이고
if(code.charAt(i-2)-'0' ==0) { // 앞 자리도 0이면
System.out.println("0"); // 0출력 후 종료
return;
}else { // 그냥 자기 자신만 0인 경우 0으로 채워준다.
dp[i][0] = 0;
}
}else // 자기 자신이 0이 아닌 경우는 경우의 수가 존재한다.
dp[i][0] = (dp[i-1][0]+dp[i-1][1]) % 1000000; // 이전 수의 0열 1열의 합
if(code.charAt(i-2)-'0'==1) { // 자신의 앞 수가 1인 경우
if(code.charAt(i-1)-'0'>=0 && code.charAt(i-1)-'0'<10) // 자신은 0~9가 가능하다.
dp[i][1] = (dp[i-2][0]+dp[i-2][1]) % 1000000; // 이전 이전 수의 0열 1열의 합
}
else if(code.charAt(i-2)-'0'==2) { // 자신의 앞 수가 2인 경우
if(code.charAt(i-1)-'0'>=0 && code.charAt(i-1)-'0'<=6) { // 0~6이 가능하다.
dp[i][1] = (dp[i-2][0]+dp[i-2][1]) % 1000000; // 이전 이전 수의 0열 1열의 합
}
}
else dp[i][1]=0; // 위의 범위에 속하지 않는 것은 경우의 수가 존재하지 않으므로 0
}
int sum =0;
for(int j=0;j<2;j++) { // 마지막 행의 0열 1열의 합이 모든 경우의 수가 된다.
sum +=dp[code.length()][j];
}
System.out.println(sum % 1000000);
}
}